Big O notation

Big O notation

Big O notation es lo que nos dice que un algorítmo es mejor que otro. Nos ayuda a determinar que implementación es más viable a mayor escala.

Nos hace estar concientes de que ciertas operaciones, estructuras de datos y uso de memoria son más eficaces que otras a mayor input. Lo que nos lleva a la escalabilidad. Cuando me refiero a escalabilidad me refiero como se ralentiza el programa debido a el aumento de input.

¿Como calculamos la escalabilidad?

Usamos Big O notation para eso, entoces en vez de estar pendiente del tiempo calculamos cuantas operaciones tiene que hacer el ordenandor para realizar determinada tarea.

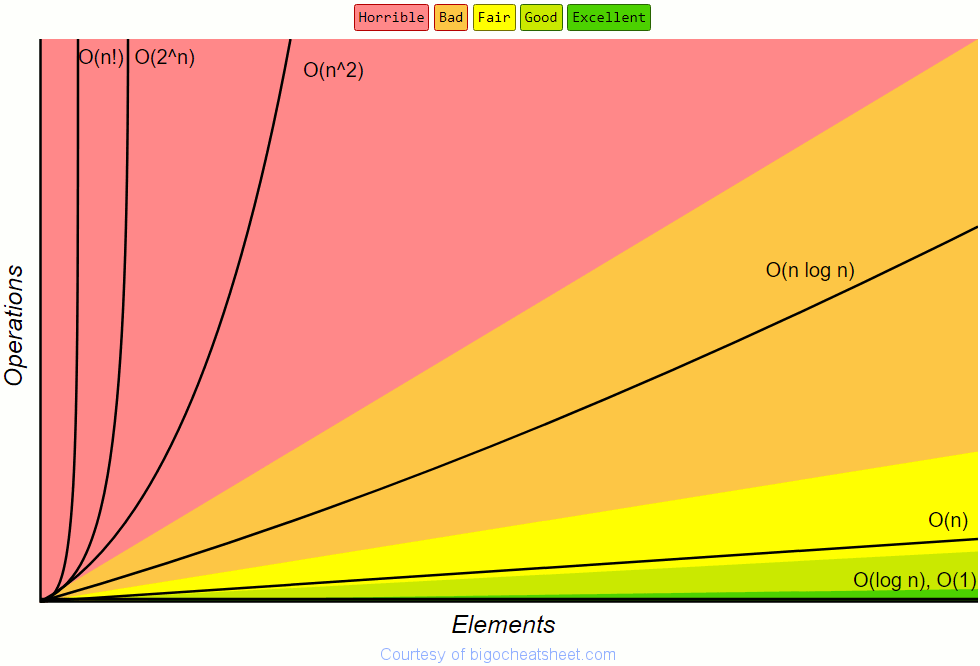
Esta es la lista de Big Os que usas para calcular:

O(1) Constant- no loops

O(log N) Logarithmic- usually searching algorithms have log n if they are sorted (Binary Search)

O(n) Linear- for loops, while loops through n items

O(n log(n)) Log Liniear- usually sorting operations

O(n^2) Quadratic- every element in a collection needs to be compared to ever other element. Two nested loops

O(2^n) Exponential- recursive algorithms that solves a problem of size N

O(n!) Factorial- you are adding a loop for every element Iterating through half a collection is still O(n) Two separate collections: O(a * b)

Ejemplos:

function getFirstPackage(package){
  return package[0] // O(1)
}

Debido a que no importa la cantidad de input que reciba solo va a trabajar con uno, solo una operación que la hace constante. Por tanto recibe un Big O de O(1)

Conclusiones

Por tanto una persona que entienda Big O notation tiene una visión más amplia no de la sintaxis de un lenguage de programmación sino de resolver problemas en general.